Lesson 1-1 - Parallel Universes
Escher's Relativity
The first allusion to parallel universes occurs very early on in the
series, in the season 1 episode I, Roommate. Bender and Fry are hunting
for apartments, when they come across one similar to M.C. Escher's
lithograph print. Bender tumbles down one of the stairways, and then
continues to fall from dimension to dimension.
Fry makes the comment, "I'm not sure we want to pay for a dimension
we're not goning to use." This contrasts with the nature of the original
work, which is meant to portray a sort of utopian structure.
Relativity (see Figure 1-1) may seem to be
an intimidating piece of art when first approached, but it has a
definite meaning. There are two gravity sources in the picture, and
three stairways that can be climbed. However, each inhabitant has a
limited amount of space in which he can move. If he were to enter a
space that did not include his original spot of gravity, he would fall
out.
Perhaps this is more relevant to
roommate than anyone, with the need for privacy gaining so much
attention in friend-friend living situations.
Figure 1-1

The Parallel Tourist Trap
The season 2 episode I Dated a Robot shows only a single parallel
universe. The only difference is that all of the inhabitants wear cowboy
hats. Other than this small (one-off joke) point, the universes are
identical right down to their events, which is exemplified with both
groups of characters being at the same place in their respective
universes.
The deepness here can be found in the
simplicity. Often in the speculative fiction genre, other universes are
seen as weird and, sometimes, chaotic. However, if the conditions in
that universe were perfect enough to foster life, then they cannot be
too dissimilar to the universe around us. Therefore, it is not entirely
far-fetched to imagine that the differences between us would be found
only in the details, such as current hat fashions.
Theories from The Farnsworth Parabox
The Farnsworth Parabox introduces some interesting ideas on the matter
of parallel universes. A total of nine are introduced, and the idea of
an infinite amount of self-producing universes is portrayed.
The main universe, or Universe A, is the most similar to our own
universe. However, in a few of the other parallel universes shown to be
connected to Universe A the differences are slight.
Universe 1 is the first universe visited, and in it the main difference
of coin flips is always the reciprocal. This is shown through the
difference in Bender A's and Bender 1's metal colors, and the difference
in Leela A/Fry A's and Leela 1/Fry 1's relationships.
Universe 3, which is not actually given a name in the episode nor is it
actually shown, seems to have the difference in its weather. Fry sticks
his head into one of the boxes, and when he takes it back out again his
had has been frozen. Universe 4, the other unnamed universe, possesses
the quality of a sort of love delirium. Professor Farnsworth sticks his
head into the box, and when he takes it out he is covered in lipstick.
The characters then proceed to explore several other universes, which
are given names related to their properties. In Universe 25, the
characters are all the same as in Universe A, aside from the fact they
do not have eyes. Universe 1729 is inhabited by bobble-head versions of
the characters; while in Universe 31 the characters are robots. Universe
XVII is only seen for a moment, and its sole inhabitant is a
toga-wearing professor that seems to be doing some sort of mathematic
problem in Roman numerals. The final destination, Universe 420 contains
obviously stoned versions of Professor Farnsworth and Amy.
These universes are not particularly interesting aside from their
comical value. Rather, it is the ending of the episode which contains
the most intriguing element. Farnsworth 1 and Farnsworth A both pull
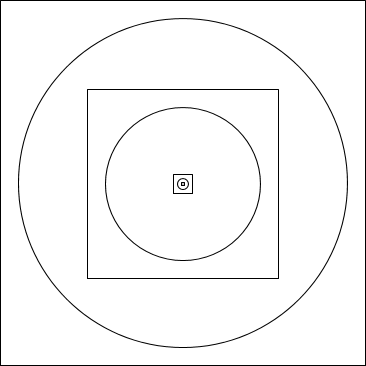
their own universes into themselves. According to a holgraphic diagram
(Figure 1-2a) created by the two Farnsworths, the box contains the
universe. But as we see in the episode, the universe also contains the
box, otherwise the box would not be visible from inside of the universe.
This creates a sort of chicken-egg chain, in which each universe
contains a box, while each box contains the universe.
However, this should not be taken as meaning each box contains an
identical universe, but that both the box is contained inside of the
universe, and vice versa. If you were to leap into the box, you would
simply be tossed back out again. This is portrayed by Figure 1-2b, in
which each square represents Box A, and each circle represents Universe
A.
Figure 1-2a

Figure 1-2b
 |





